
高校数学a 三角形の面積比 等高 等底 等角 受験の月
それでは、塩水の相似比、面積比、体積比の算出に慣れるためにも、練習問題を解いていきましょう。 例題 辺の長さの比(相似比)が3:2である円錐の体積比はいくつになるでしょうか。 解答 上の計算式を利用していきます。次の図の abcと adeのように,1つの角(∠a)が共有されている2つの三角形の面積比について考えます。 ABCと ABEは,頂点Bが共通なので,底辺の比と面積比が等しくなり,

高校数学a 三角形の面積比 等高 等底 等角 受験の月
それでは、塩水の相似比、面積比、体積比の算出に慣れるためにも、練習問題を解いていきましょう。 例題 辺の長さの比(相似比)が3:2である円錐の体積比はいくつになるでしょうか。 解答 上の計算式を利用していきます。次の図の abcと adeのように,1つの角(∠a)が共有されている2つの三角形の面積比について考えます。 ABCと ABEは,頂点Bが共通なので,底辺の比と面積比が等しくなり,
各面積の計算方法 外壁や屋根塗装の見積りは、「塗る部分の面積 x 塗料の単価」で決まります。 そのため、 一部の悪徳業者は、見積り金額を高くするために塗る部分の面積を大きめに出す業者もおります 。 このような場合、自分である程度の面積をの面積に相当します。 面積の単位を扱う時は次のようにどの部分を2乗しているのか気をつけてください。 したがって、面積の単位には、m 2 、km 2 、cm 2 のように必ず2を付けなければいけないことを覚えておきましょう。など、計算する順番を決めておきます。 この正負によって、各台形の面積の正負が決まります。 この例では、1で計算をすすめます。 台形の面積の公式は、 台形の面積=(上辺下辺)¶高さÖ2 なので、 S1=(Y2Y1)¶(X1X2)Ö2で求積できます。
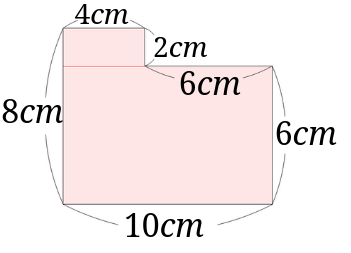
小学4年生で習う長方形や正方形の面積の応用問題を解説 みけねこ小学校
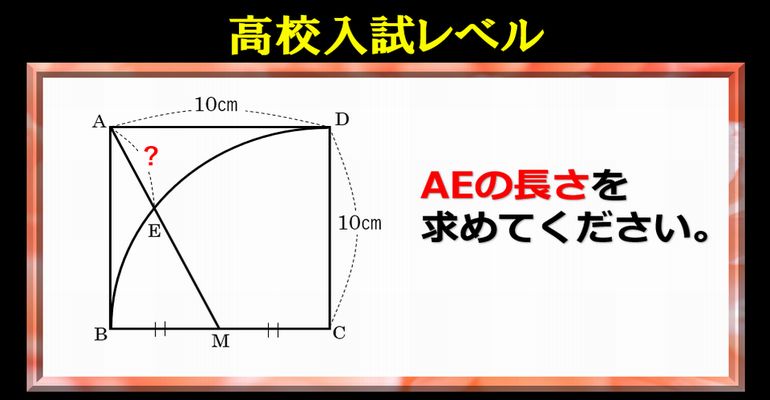
高校入試レベル 数学図形の良問 三平方の定理などを使って考えてみてください ネタファクト
三平方の定理を用いるこの例題を解くことで三平方の定理の問題が少し好きになれました! ありがとうございます!! この調子で高校入試に望みたいと思います!! また違う問題などをあげていただけるとこちらとしても幸いです! 三平方の定理の特別三角形の1対1対ルート2と1対2対ルート3の意味がわからないので わかるかたは教えてください 高校 締切済 教えて!goo
